Static and Dynamic Lower Bounds on Utilities
Looking ahead to one of Chapter 4’s impacts on action TUFs—in dynamically real-time systems, it may be that just accrued utility is not necessarily the appropriate utility factor in the action sequencing optimality (more generally, satisficing) criterion. For example, suppose:
- action A1 can be sequenced to achieve U1= 4 of its maximum of 7
• action A2 can be sequenced to achieve U2 = 3 of its maximum of 5
• producing accrued utility U12 = 7
• and this causes action A3
– to be sequenced to achieve only U3 = 3 of its maximum of 15
– or even not to be sequenced at all
- even though A3 has higher maximum utility (15) than
– either A1 (7) or A2 (5)
– the maximum possible accrued utility from A1 + A2 (7 + 5 = 12 < 15)
- which is likely to be undesirable, and indicates that accrued utility as defined thus far may not always adequately represent the utility relationships among actions.
Thus often, action TUF’s must provide for specifying that individual actions each achieve at least a lower bound on their maximum possible utilities. Given that, they must also provide for specifying a lower bound on the accrued utility of multiple TUF’s.
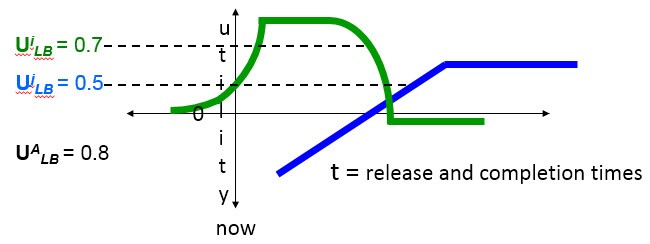
A TUF may specify a lower bound on its maximum utility
and a lower bound on the accrued utility of multiple TUF’s
Since usually dynamically real-time actions (and systems) are subject to inherent dynamic uncertainties in their applications and operational environments, it is more realistic to specify lower bounds on individual and accrued utilities non-deterministically.
The most obvious method of specifying, and formally reasoning about (e.g., for sequencing), these uncertain lower bounds is based on a probability theory. Various theories of probability are introduced in Chapter 3 of the book because the most widely used frequentist one is not the best, and is actually often the worst, for this purpose. However, the frequentist theory is depicted here because it is the easiest to relate to, and has consequently been widely used in TUF theory and practice.
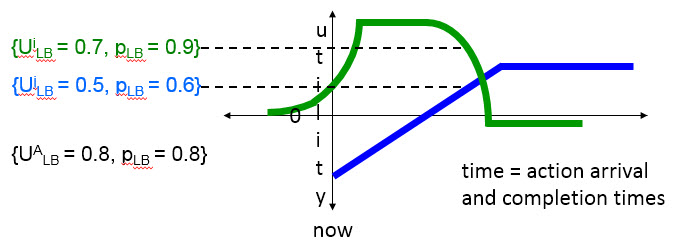
A TUF may specify probabilistic lower bounds on its maximum utility
and on the accrued utility of multiple TUF’s
