Time/Utility Functions
“The problem is never
how to get new, innovative thoughts into your mind,
but how to get old ones out.”
—Dee Hock, The Birth of the Chaordic Age
To reason about a dynamic real-time action, the relationship between all of its possible completion times and a metric for completion time preference has to be made formally explicit. There is a variety of ways to express that relationship. The one discussed here is functionally—particularly time/utility functions (TUFs) [ ], (originally called benefit [ ], and then time/value [ ], functions)—which is one naturally expressive way.
An action TUF is derived from the application and relates the action’s completion in its context’s physical time to the consequential gain or loss of utility in some application-specific metric.
For example, an action having a traditional hard real-time deadline has the maximum utility of 1 (by convention) if the action completes before or at the deadline, and the minimum utility of 0 (by convention) if the action completes after the deadline. So the traditional hard real-time deadline is binary unit-valued downward step function f(tc)=1 for all tc ≤ td, and 0 otherwise. The step is a downward inflection point of the function.
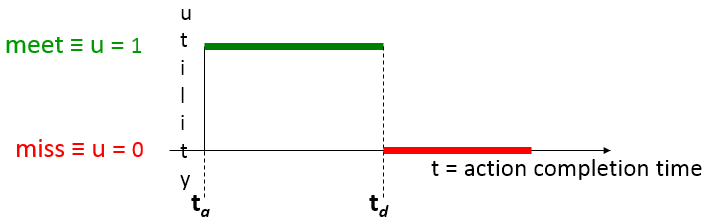
The traditional hard real-time deadline
is equivalent to a binary unit-valued downward step function
This graphical function depiction is insightful because it immediately reveals how to begin generalizing from an action having a traditional hard deadline, to a dynamic real-time action.
The conventional real-time computing system viewpoint erroneously associates specific semantics, based on two special case assumptions, with the syntax of a deadline—that an action (i.e., computational task) which misses its deadline despite being admitted by the usual á priori admission control (e.g., rate monotonic analysis) has failed and is terminated. As stated above, this confuses the syntax and semantics of a time constraint.
But in general, an action which misses its deadline usually has some application- or situation-specific residual utility to the system. That utility may be either sub-optimally positive, as for action A1, or negative, as for action A2. The functional representation provides a formal means of reasoning about such cases:
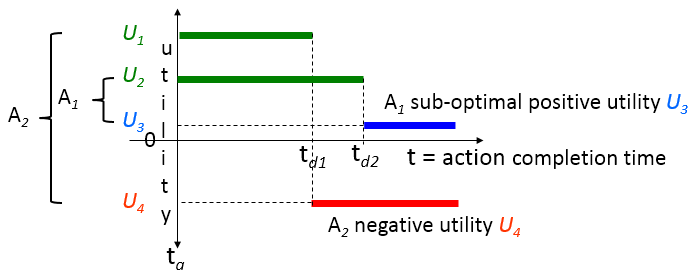
In general, an action which misses its deadline
may have some residual positive or negative utility
Residual positive utility is more common than not in human lives and automated systems, so examples are obvious. Perhaps less obviously, in general, negative utility cannot be rejected as contradictory since there are cases where its magnitude is needed—e.g., to make adjustments for either retrying the action or performing alternative action(s).
A real-time-action’s TUF does not necessarily have a binary valued discontinuity at its deadline time, as corresponding TUF’s for traditional deadlines do. It may have application- or situation-specific continuously changing amounts of, and transitions to, positive and/or residual utility after the deadline time. Referring back to previous examples: tardiness in picking your child up from school, or sending an interceptor missile course update, may have positive residual utility at some decreasing rate, beginning at an arbitrary tx—and possibly negative utility (constant or increasing) after the action reaches the deadline td.

A dynamic action’s TUF generally is not
a binary-valued downward step function
Without elaborating many various possible TUF’s here, a representative group commonly used in my application experiences are depicted below.
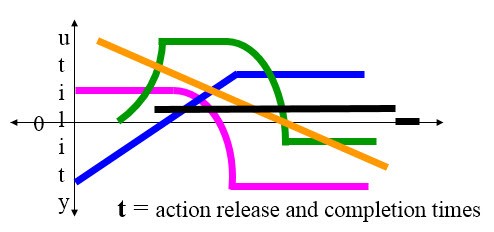
A variety of some representative popular concave downward TUF’s
Note that the TUF depicted in black is the special case of the conventional binary unit-valued deadline.
TUF’s that are concave downward (a linear one is considered to be)—i.e., once a TUF has decreased utility, subsequent increases are not valid—are much easier to reason about and sequence, and so this abbreviated preview will focus on only those.
Three linear TUF’s merit further observation.
A linearly decreasing TUF can be interpreted as meaning that its action should be completed as soon as possible. A linearly increasing TUF can be interpreted as being for an action that results in greater utility the longer it operates—there are numerous algorithms (e.g., searching) and applications (e.g., radar report correlation) for which this is true.
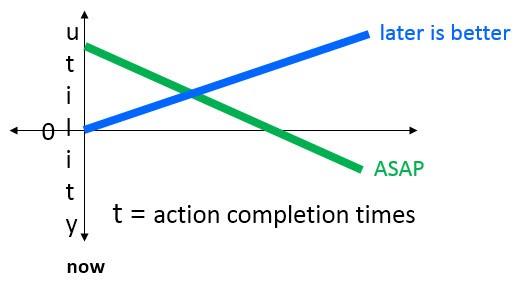
Linearly increasing or decreasing TUF’s
Horizontal TUF’s denote actions which have no time constraint—i.e., are non-real-time—but their positive utilities can represent relative importance for sequencing them in a multiplicity of actions. That has the major advantage of managing both time-constrained (real-time) and non-time constrained (non-real-time) actions with the same sequencing abstraction and algorithms. In this document, for simplicity, negative importance for horizontal TUF’s is undefined. (In general, importance is orthogonal to urgency, and negative importance is valid.)
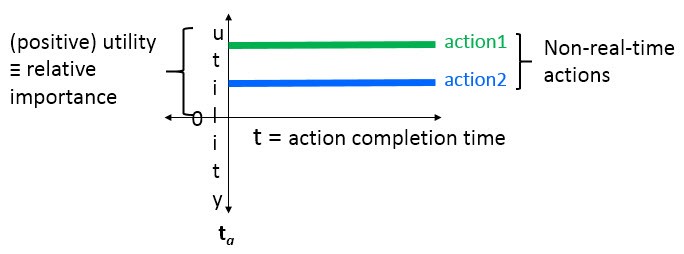
Both real-time and non-real-time actions
can be managed together coherently using TUF’s
Looking forward to describing actions’ timeliness using TUF’s at the dynamic real-time system level in Chapter 4, TUF’s are sequenced based primarily (but not exclusively) by seeking to maximize accrued (for example, but not limited to, summed) utility Ua for all sequenced actions’ utilities Ui:
![]()
This criterion can be couched as an instance of the well-known Gittins index [ ] approach to the multi-armed bandit problem [ ], or as a Markov decision problem, as discussed in Chapter 4.
Utility accrual sequencing can take into account not just preferences of action sequences based on timeliness and other criteria, but also intensity of preferences—e.g., frequently with application-specific TUF weights, as summarized in the excerpts from Chapter 4 of the book.
